
Although I continue my practice of algorithms, I am still having trouble identifying when to use the appropriate data structure. I recently attempted to solve a problem on LeetCode and completely missed the obvious hints that a queue would be a good data structure to use for the algorithm. This post will provide a detailed solution with illustrations for that problem. While the main purpose of this post is to help others get a clear mental picture of what is happening with the algorithm, I also write this post with the hope that I can work to strengthen my intuition of when to leverage the correct data structure.
The Problem
In a deck of cards, every card has a unique integer. You can order the deck in any order you want.
Initially, all the cards start face down (unrevealed) in one deck.
Now, you do the following steps repeatedly, until all cards are revealed:
- Take the top card of the deck, reveal it, and take it out of the deck.
- If there are still cards in the deck, put the next top card of the deck at the bottom of the deck.
- If there are still unrevealed cards, go back to step 1. Otherwise, stop.
Return an ordering of the deck that would reveal the cards in increasing order.
The first entry in the answer is considered to be the top of the deck.
Example
Input: [17, 13, 11, 2, 3, 5, 7]
Output: [2, 13, 3, 11, 5, 17, 7]
Explanation:
- We get the deck in the order [17,13,11,2,3,5,7] (this order doesn’t matter), and reorder it.
- After reordering, the deck starts as [2,13,3,11,5,17,7], where 2 is the top of the deck.
- We reveal 2, and move 13 to the bottom. The deck is now [3,11,5,17,7,13].
- We reveal 3, and move 11 to the bottom. The deck is now [5,17,7,13,11].
- We reveal 5, and move 17 to the bottom. The deck is now [7,13,11,17].
- We reveal 7, and move 13 to the bottom. The deck is now [11,17,13].
- We reveal 11, and move 17 to the bottom. The deck is now [13,17].
- We reveal 13, and move 17 to the bottom. The deck is now [17].
- We reveal 17. Since all the cards revealed are in increasing order, the answer is correct.
Some Thoughts
Before we get to the optimal solution, I wanted to briefly talk about my attempted solution.
My solution only works for the example test case. I was too focused on trying to transform the provided input into the target output. I did not take enough time to consider all possible test cases, or at the very minimum at least test cases of different lengths.
I think it would have helped if I had slowed down a bit. I should have thought more about the problem and asked myself which data structures would be good candidates. A stack or a queue should have been an obvious choice for a problem that is about a deck of cards.
The optimal solution for this problem uses a queue. If you need a refresher on queues then check out this post about queues. The solution will also be storing index values inside of the queue. This is a great technique and I definitely want to get better at recognizing when it is appropriate to use. Here is an algorithm that uses that technique except with a stack.
How to Solve
The solution that will be covered was submitted by LeetCode user @caraxin. Here is the submission. Here are the steps:
- Sort the deck, it is actually the “final sequence” we want to get according to the question.
- Then put it back to the result array, we just need to deal with the index now!
- Simulate the process with a queue (initialized with 0,1,2…(n-1)), now how do we pick the card?
- We first pick the index at the top: res[q.poll()] = deck[i]
- Then we put the next index to the bottom: q.add(q.poll())
- Repeat it n times, and you will have the result array!
The Code
Here is the code for the @caraxin approach. As you can see, the solution is quite succinct and does an amazing job of utilizing a queue. Super smart!
Some Illustrations
This is a perfect problem to use some illustrations to get a clear mental picture of what is going on.
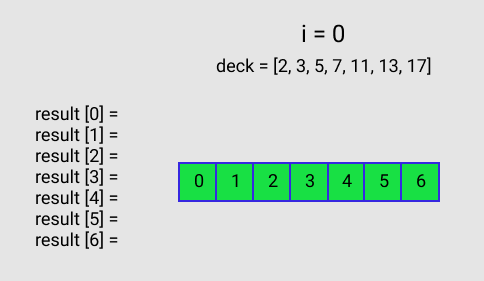
Figure A just shows the initial setup. The queue is filled with index values 0-6, result is initialized, and i = 0. deck has been sorted.
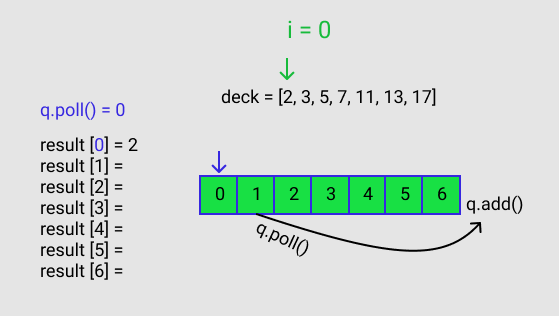
q.poll() gives a value of 0. This 0 corresponds to the index for result. result[q.poll()] = deck[i] == result[0] = deck[0]. q is polled again and that polled value is added to the queue. This is shown in Figure B.
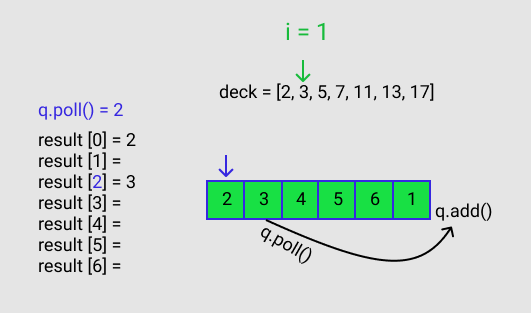
q.poll() gives a value of 2. This 2 corresponds to the index for result. result[q.poll()] = deck[i] == result[2] = deck[1]. q is polled again and that polled value is added to the queue. This is shown in Figure C.
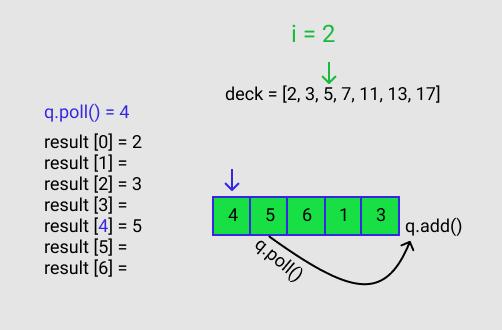
q.poll() gives a value of 4. This 4 corresponds to the index for result. result[q.poll()] = deck[i] == result[4] = deck[2]. q is polled again and that polled value is added to the queue. This is shown in Figure D.
q.poll() gives a value of 6. This 6 corresponds to the index for result. result[q.poll()] = deck[i] == result[6] = deck[3]. q is polled again and that polled value is added to the queue. This is shown in Figure E.
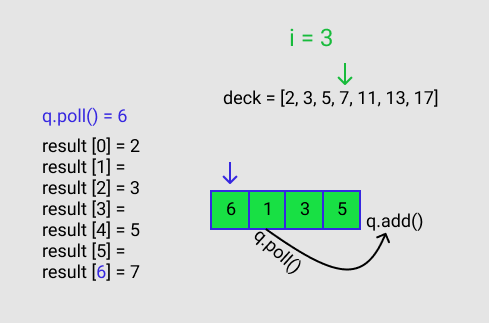
q.poll() gives a value of 3. This 3 corresponds to the index for result. result[q.poll()] = deck[i] == result[3] = deck[4]. q is polled again and that polled value is added to the queue. This is shown in Figure F.
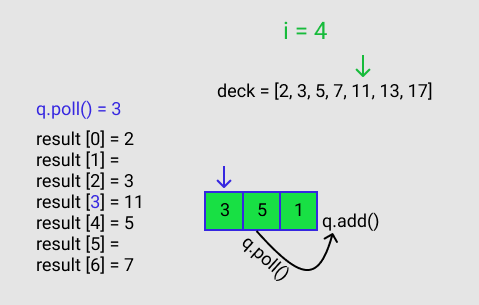
q.poll() gives a value of 1. This 1 corresponds to the index for result. result[q.poll()] = deck[i] == result[1] = deck[5]. q is polled again and that polled value is added to the queue. This is shown in Figure G.
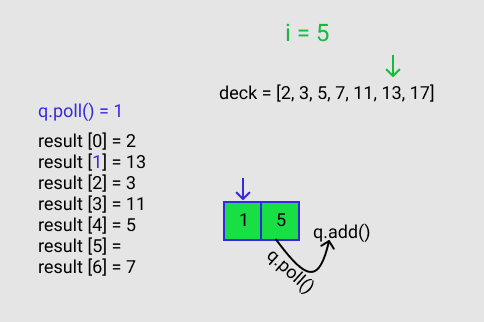
q.poll() gives a value of 5. This 5 corresponds to the index for result. result[q.poll()] = deck[i] == result[5] = deck[6]. There are no additional values to poll from the queue. This is shown in Figure H.
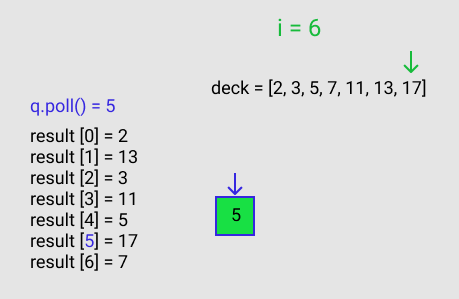
result: [2, 13, 3, 11, 5, 17, 7]
Time Complexity
The time complexity of this algorithm is O(n * log(n)), where ‘n’ is the number of cards in the deck. Let’s go over this a bit.
The array is sorted. Now I think that it depends on the version of Java, but either Timsort, or Dual-Pivot QuickSort is used for Arrays.sort(). This is O(n * log(n)). This might help explain it better too.
Then we need to iterate the length of n to add the index values to the queue. This is O(n). This gives O(2n * log(n)). Then the length of n needs to be iterated for adding the values to result. This is O(n). This gives O(3n * log(n)). The constant is dropped giving O(n * log(n)).
Space Complexity
The space complexity will be O(n). Let’s break it down like we did for the time complexity.
O(n) is required for the result array. O(n) is required for the queue. O(n) is required for the sorting. This totals to O(3n). The constant is then dropped giving O(n).
If you are looking for more tips and tricks for Big-O then you might find this post helpful.
Get Better at Algorithms!
Algorithms and data structures are pretty tough. They are definitely taking a while for me to get the hang of them. However, there are some great resources out there, and I feel obligated to share some that have been most helpful to me. If I missed any that have been helpful to you, be sure to mention them in the comments.
- Cracking the Coding Interview – Great resource. Really gets you in the right mindset for interviews. You can find it here.
- Elements of Programming Interviews – Another great book. Personally, I like this one more than CTCI, but YMMV. You can find it here.
- Grokking the Coding Interview – Can’t emphasize this one enough. Haven’t seen it mentioned it too often. Explains patterns that occur in different coding challenge problems. Great at providing a big-picture of all the different algorithm problems you might encounter. Check it out here.
- Grokking Dynamic Programming – Dynamic programming is tough. This course has definitely helped me get a better understanding.
- Tushar Roy – Tushar really knows his stuff. His dynamic programming playlist is especially good. Check out his awesome YouTube channel.
- Back To Back SWE – Great YouTube Channel. Highly recommend.
- Kevin Naughton Jr. – Another awesome YouTube channel. Great at going over problems and gives helpful advice.
- Base CS – Vaidehi Joshi does a great job of laying out the fundamentals of algorithms and data structures. Check out the blog series here. She also has a podcast that I give two thumbs up.
- Coding Challenge Website – There are plenty of different ones to choose from. HackerRank, CodeWars, and Edabit all seem to be pretty popular. I personally use LeetCode. Find the one that works for you!
- Pramp – Do mock interviews! The sooner the better! Pramp has been a huge help to me.
Well, I hope that was useful. Thanks for reading my post and best of luck with your learning about data structures and algorithms!